Ramanujan’s Pi Reveals a Hidden Universe

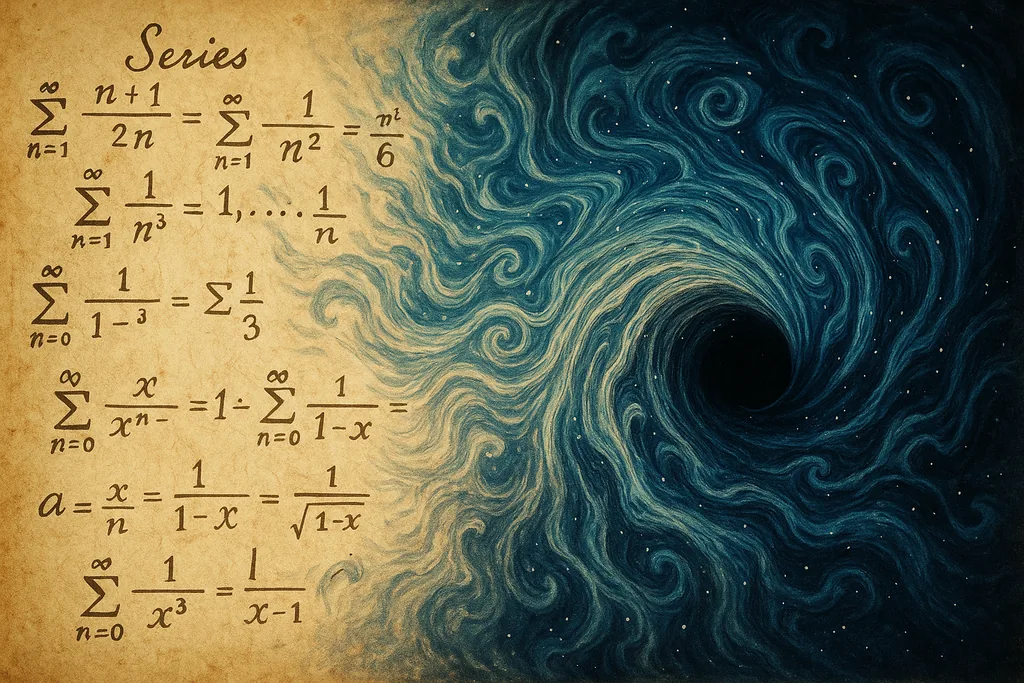
Century-old formulas, modern universes

On 4 December 2025, a team at the Indian Institute of Science (IISc) in Bangalore published a striking observation: a set of compact, 100‑year‑old series Srinivasa Ramanujan wrote for calculating π turns up naturally inside the mathematics physicists use to describe scale‑invariant systems, including models for turbulence, percolation and certain black‑hole problems. The discovery links two traditions often treated as separate — Ramanujan’s fiercely inventive number theory and the analytic machinery of contemporary high‑energy physics — and points to a deeper unity behind apparently unrelated phenomena.

Ramanujan’s formulas and why they mattered

From scale invariance to logarithmic conformal field theories

Conformal field theory is the language physicists use to describe systems that look the same at every scale. Think of the point where water becomes indistinguishable between liquid and vapour, or the fine structure of certain phase transitions: zoom in or out and the pattern resembles itself. Those scale‑invariant systems are not just curiosities of condensed matter — they form a bridge into string theory, statistical mechanics and parts of quantum gravity.

Working within a subfamily called logarithmic conformal field theories, the IISc researchers found the hallmarks of Ramanujan’s π‑series embedded in the formulas physicists use to compute observables. Logarithmic CFTs are mathematical beasts that appear when conventional CFT techniques need to be modified to handle more subtle correlations — for instance in problems of percolation (how clusters form in disordered media) and in descriptions of certain black‑hole microphysics. In these models the same compact combinations of functions and coefficients that Ramanujan wrote down crop up naturally, as if the physical symmetry had been whispering the same mathematics a century earlier.

Computation, efficiency and conceptual payoff

One practical consequence of this match is computational: the researchers report that exploiting the Ramanujan‑style structure allows them to compute key theoretical quantities more efficiently than with more blunt, conventional techniques. The analogy the team draws is direct — the way Ramanujan’s series accelerate digit‑by‑digit computation of π, so similar patterning can accelerate the extraction of quantities that matter to physicists studying critical phenomena or black‑hole‑related calculations.

That gain is not merely a numerical trick. It points to a conceptual economy: when the same mathematical pattern appears in two distinct domains, it often means there is a unifying principle waiting to be articulated. For pure mathematicians the appearance of Ramanujan’s series in physics is a pleasing echo; for physicists it is a reminder that the toolbox of pure mathematics may already contain precisely the functions and identities needed for thorny calculations.

What this tells us about black holes and turbulence

The headlines will naturally gravitate to "black holes," and for good reason: the mathematics that encodes some aspects of black‑hole physics — especially problems where conformal symmetry or its cousins provide a useful description — can be recast using the same functional structures Ramanujan used. That does not mean Ramanujan anticipated black‑hole physics in a modern sense; rather, it shows that his identities pick out a corner of mathematical structure that physicists later found essential for describing a range of scale‑invariant phenomena, including regimes that model black‑hole behaviour.

Similarly, turbulence and percolation are famously hard problems because they mix many scales and unpredictable interactions. The fact that logarithmic CFT frameworks that physicists employ for simplified or idealised versions of these problems carry Ramanujan‑like series suggests new analytic handles on long‑standing theoretical headaches. Researchers can potentially use these series to reorganise perturbative expansions or to evaluate special functions with greater accuracy and less computational overhead.

Mathematics, physics and the long reach of ideas

There is a narrative appeal to this result: a solitary mathematician in early‑20th‑century India produced equations so tightly crafted they later turn up in mathematical models of black holes and fluid chaos. But the scientific lesson is subtler. Deep mathematics tends to be resilient and transferable. Identities and structures that first arise in number theory or complex analysis often resurface in physical theories because both disciplines, at their cores, are searching for ways to organise patterns and symmetries.

The IISc work underscores the value of cross‑disciplinary literacy. A mathematical trick developed to push the limits of π calculation becomes a computational shortcut in a physically motivated calculation; a physical theory highlights previously unnoticed relations among special functions. It is an invitation — to mathematicians to look for physical realisations of abstract identities, and to physicists to mine classical mathematics for tools that simplify their models.

Next steps and open questions

The immediate technical follow‑ups are straightforward: map which Ramanujan series correspond to which classes of observables in logarithmic CFTs, and test whether the computational advantages persist in increasingly realistic models of turbulence or black‑hole microphysics. On a broader level, the result raises a tantalising question: which other classical mathematical constructions hide in the formalism of modern physics, waiting to be rediscovered?

Answers will require sustained dialogue between analysts, number theorists and field theorists — and perhaps more importantly, the humility to let apparently esoteric identities lead the way. If one century’s arithmetic curiosity can illuminate a universe of physical behaviour a hundred years later, then the boundary between "pure" and "applied" mathematics looks less like a wall and more like a porous membrane through which insight freely flows.

For now, the IISc finding is a reminder that progress in fundamental science is often recombinant: old ideas recombined with new contexts can open routes that neither discipline could foresee on its own.